Jos olet joskus kuullut E8 ryhmästä tai yrittänyt ottaa selvää Garret Lisin maailmankaikkeuta selittävästä teoriasta olet mahdollisesti törmännyt seuraavan kaltaisiin tähtikuvioihin:
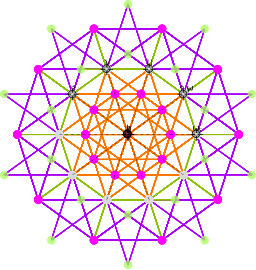
Kyse on hyvin moniulotteisesta hyperkuutiosta, tässä on hieman yksinkertaisempi esimerkki hyperkuutiosta (4 ulotteinen):
Mitä tämä tarkalleen ottaen tarkoittaa? Jos lähdetään liikkelle yksinkertaisimmasta esimerkistä niin aluksi meillä on jana, lisätään yksi ulottuvuus niin janoista voidaan muodostaa neliö. Jatketaan ja lisätään vielä ulottuvuus niin voidaan neliöistä muodostaa 3 ulotteinen kuutio:
Mutta miten seuraava 4 ulottuvuuden kuvio hyperkuutio oikein muodostuu?
Samalla tavalla kuin kuution kuva tasossa on projektio oikeasta 3 ulotteisesta kuutiosta 2 ulottuvuuteen on myös hyperkuution kuva projektio 4 ulotteisesta hyperkuutiosta 2:een ulottuvuuteen.
Piirretään uusi koordinaattiakseli z joka on kohtisuorassa x ja y koordinaattiakseleita vastaan ja sen jälkeen piirretään uusi samankaltainen xy tason suuntainen neliö z akselilla kohtaan, joka on neliön sivun etäisyydellä origosta:
Nyt vain piirretään uudet neliöt (4 kappaletta) ensimmäisen ja toisen neliön väliin, nyt meillä on kuutio:
No sitä varten piirretään ensin 3 ulotteinen koodinaatisto ja siihen kuutio ja sitten taas neljäs koordinaatti akseli, nimetään se w-akseliksi, joka on kohtisuorassa kaikkia edellisiä akseleita kohtaan, ja piiretään sille taas kuutio joka on kuution sivun pituuden etäisyydellä alkuperäisestä kuutiosta.
Yhdistetään kaikki kuutioden vastaavat tahkot uusilla kuutioilla, tämä vastaa sitä kun aikaisemmassa esimerkissä yhditettiin kahden neliön sivut uusilla neliöillä ja muodostettiin kuutio. Nyt siis vain yhdistetään kahden kuution tahkot uusilla kuutioilla:
kun kolmiulotteisessa tapauksessa neliöiden väliin jäi 3 ulotteinen tila, niin nyt kuutioiden väliin jää jännä 4 -ulotteinen tila
